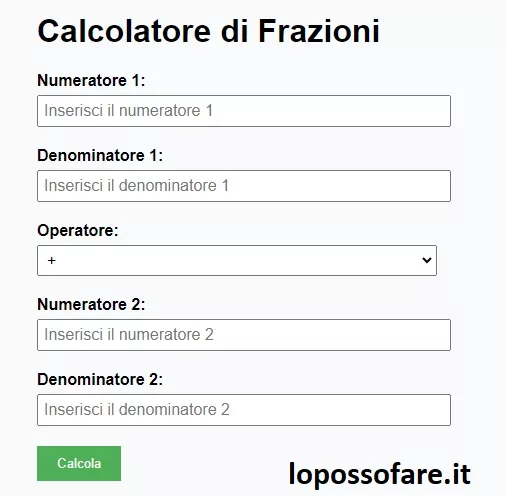
Calcolatore di Frazioni Un semplice strumento online
Le frazioni rivestono un ruolo fondamentale nel campo della matematica, trovando ampie applicazioni in situazioni reali come la suddivisione di un terreno o la spartizione di una pizza. Tuttavia, il calcolo delle operazioni con le frazioni può essere complesso e richiedere un notevole impegno di tempo. Per semplificare questo processo, è stato sviluppato un pratico […]
Calcolatore di Frazioni Un semplice strumento online Leggi tutto »