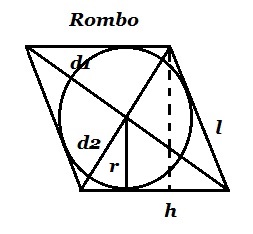
Area del rombo
Area del rombo. Il rombo è una figura piana quadrilatero ( poligono ) che ha i quattro lati uguali ( congruenti ) e le diagonali possono essere diverse e definite in diagonale maggiore, e diagonale minore.
Gli angoli possono essere di gradi diversi.
Il centro del rombo è il punto dove si incontrano le due diagonali, quella maggiore e minore.
Le lunghezze delle diagonali variano col variare degli angoli.
Se la figura risulta più schiacciata
i suoi angoli saranno due ottusi e due acuti. I due angoli contrapposti, uno di fronte all’altro, sono uguali. Angolo acuto ha un ampiezza minore di 90 gradi, quello ottuso se l’ampiezza è maggiore di 90 gradi.
Nella nostra tabella trovate tutte le formule dirette e indirette per ricavare : Area del rombo, le diagonali, lati e tutto quello che appartiene al rombo.
Le varie formule del rombo
| Formule del Rombo |
||
| Perimetro del Rombo |
P = L x 4 |
|
| Lato da Perimetro |
L = P : 4 |
|
| Area del Rombo da Diagonali |
A = d1 x d2 : 2 | |
| Diagonale maggiore | d1 = 2 x A : d2 |
|
| Diagonale minore |
d2 = 2 x A : d1 | |
| Area del Rombo da Lato e raggio |
A = L x 2r | |
| Lato |
L = A : 2r | |
| Raggio della circonferenza iscritta |
r = A : 2L | |
| Lato da diagonali (teorema Pitagora) |
L = √ (d1:2)² + (d2:2)² | |
| Semi diagonale maggiore |
d1 : 2 = √ L² – (d2 : 2) ² | |
| Semi diagonale minore |
d2 : 2 = √ L² – (d1 : 2) ² | |
| Altezza del Rombo |
h = A : L | |
Sostituire la cinghia della tapparella video guida
Da tener presente che l’altezza del rombo, è il doppio della misura del raggio della circonferenza iscritta all’interno del Rombo. Cosa che possiamo notare osservando la figura, il diametro del cerchio tocca i due lati opposti misurando l’altezza stessa. Quindi tracciando un cerchio all’interno del rombo, ricavandoci il raggio possiamo risalire all’altezza del rombo.
